How to Find the Apothem: A Guide to Geometric Calculations

Understanding geometric concepts is an essential part of mathematics and has practical applications in various fields. One such concept is the apothem, which plays a crucial role in geometry, particularly when dealing with polygons. In this guide, we will explore what an apothem is and provide step-by-step instructions on how to find it.

1. Introduction to the Apothem

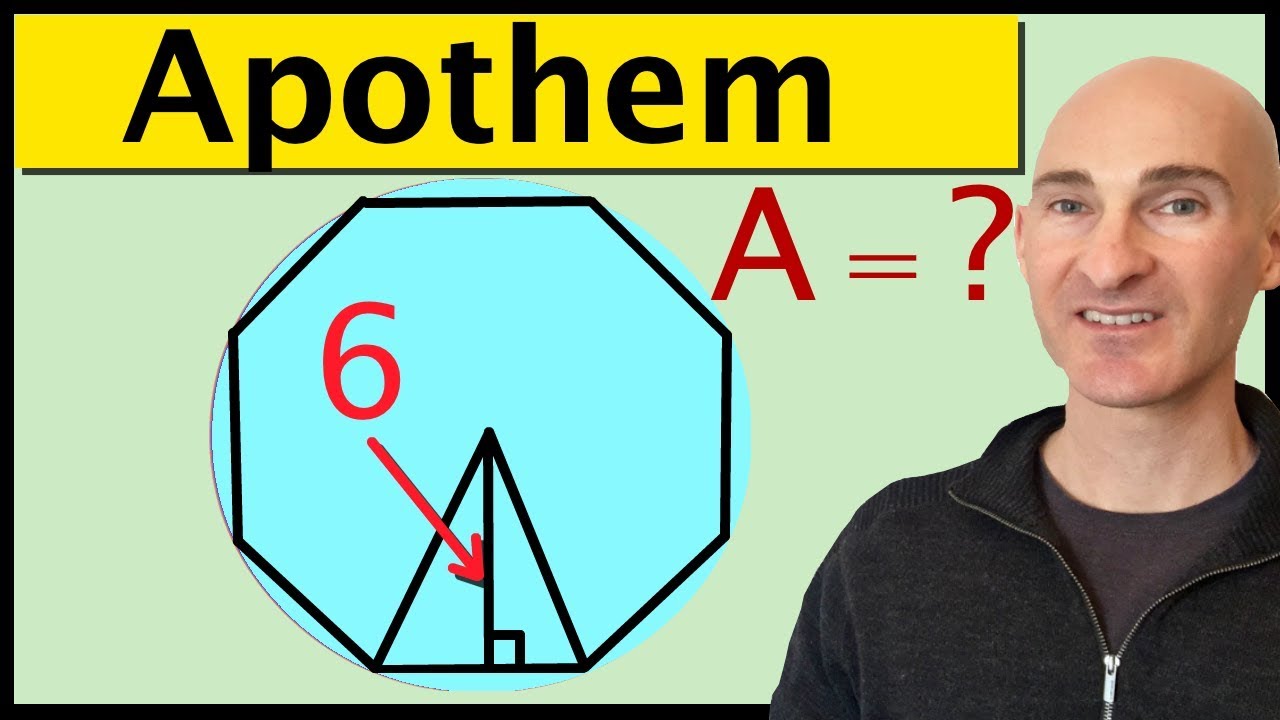
Apothem

The apothem is a geometric term used to describe the distance from the center of a regular polygon to the midpoint of any one of its sides. It is a fundamental element in the calculation of the area and other properties of regular polygons, such as triangles, squares, pentagons, and hexagons.

2. Types of Polygons with Apothems

Before we delve into how to find the apothem, let's clarify which polygons have apothems:

Regular Polygons: These are polygons with equal side lengths and equal interior angles, such as regular triangles, squares, pentagons, and so on.

Irregular Polygons: Irregular polygons do not have an apothem because they lack the uniformity of regular polygons.

3. Finding the Apothem of a Regular Polygon

To find the apothem of a regular polygon, you'll need to know the length of the polygon's side (s) and the number of sides (n). Follow these steps:

Step 1: Draw the regular polygon and identify the center.

Step 2: Draw a line from the center to one of the polygon's vertices to create a right triangle.

Step 3: Calculate the measure of the central angle (θ) by dividing 360 degrees by the number of sides (n). This angle is formed between the center, a vertex, and the midpoint of a side.

Step 4: Use trigonometric functions, such as tangent, to find the apothem. The formula for finding the apothem (a) is:

Code 1

Step 5: Calculate the apothem using the values you have gathered.

4. Practical Example

Let's take a practical example to illustrate how to find the apothem of a regular polygon. Suppose we have a regular hexagon (n = 6) with a side length of 8 units (s = 8). Using the formula above:

Step 3: The central angle (θ) is 360 degrees / 6 = 60 degrees.

Step 4: Plug the values into the formula:

Code 2

Step 5: The apothem of the regular hexagon is approximately 6.93 units.

5. Applications of the Apothem

The apothem is a critical component in calculating the area of regular polygons. For instance, to find the area of a regular polygon, you can use the formula:

Code 3

Knowing the apothem also helps in various real-world scenarios, such as architecture, engineering, and design, where precise measurements and geometric calculations are required.

Understanding how to find the apothem of a regular polygon is a valuable skill in geometry and mathematics. It enables you to calculate important properties of polygons, such as their area, and has practical applications in numerous fields. By following the steps outlined in this guide, you can confidently determine the apothem of any regular polygon you encounter in your studies or daily life.