Applying the Secant and Tangent Segment Theorem: Finding the Equation

In geometry, the Secant and Tangent Segment Theorem is a useful tool for determining relationships between segments formed by secants and tangents intersecting a circle. By understanding this theorem and its application, we can solve for unknowns and establish equations that describe the given figure. In this article, we will explore the application of the Secant and Tangent Segment Theorem and determine the resulting equation.

 

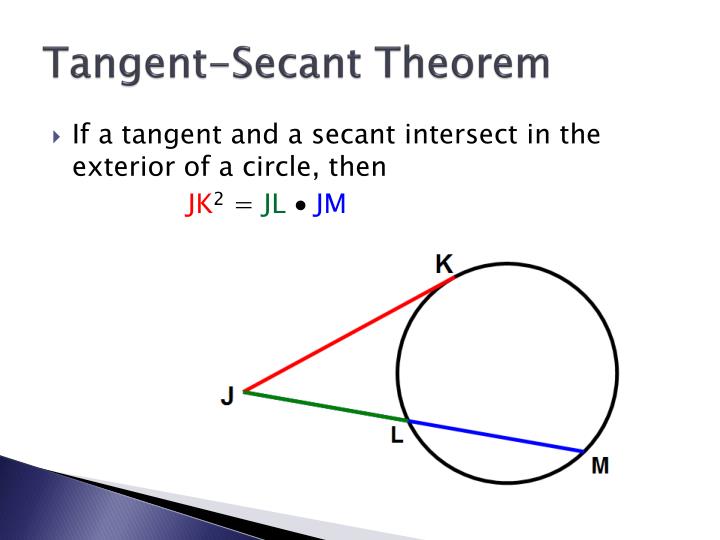
Tangent - Secant Theorem

 

 

 

1. Understanding the Secant and Tangent Segment Theorem:

 

The Secant and Tangent Segment Theorem states that when a secant and a tangent intersect outside a circle, the product of the entire secant segment and its external segment is equal to the square of the tangent segment. Mathematically, it can be expressed as follows:

 

(Secant Segment)(External Segment) = (Tangent Segment)^2

 

2. Analyzing the Given Figure:

 

To apply the Secant and Tangent Segment Theorem, we need a specific figure or scenario. Let's consider a circle with a tangent and a secant intersecting outside the circle.

 

3. Determining the Equation:

 

Let's assign variables to the segments in the figure for clarity. Suppose:

 

• The secant segment is denoted as 'a'.
•  
• The external segment of the secant is denoted as 'b'.
•  
• The tangent segment is denoted as 'c'.
•  

Applying the Secant and Tangent Segment Theorem, we have: (a)(b) = (c)^2

 

This equation represents the relationship between the segments in the given figure.

 

4. Solving for Unknowns:

 

Depending on the given information, we can use the equation to solve for unknown variables.

 

By substituting known values and rearranging the equation, we can determine the values of the segments in the figure.

 

5. Example Application:

 

Let's consider an example where the secant segment 'a' has a length of 6 units, and the external segment 'b' has a length of 4 units.

 

We can substitute these values into the equation: (6)(4) = (c)^2

 

Simplifying the equation gives us: 24 = (c)^2

 

Taking the square root of both sides, we find that: c = √24

 

Thus, the length of the tangent segment 'c' is approximately 4.899 units.

 

6. Generalizing the Equation:

 

The equation derived from the application of the Secant and Tangent Segment Theorem is not limited to specific values. It holds true for any given figure where the segments satisfy the conditions of the theorem.

 

 

 

Secant

 

 

 

The Secant and Tangent Segment Theorem provides a valuable tool for understanding the relationships between secant and tangent segments in a circle. By applying this theorem, we can establish equations that describe the given figure and solve for unknown variables. Understanding and utilizing the theorem allows us to explore geometric concepts and solve real-world problems involving circles and their tangent and secant lines.