Which Best Describes the Range of the Function f(x) = 2(3)^x? Unveiling the Function's Behavior

In the realm of mathematics, functions play a fundamental role in describing relationships between variables. Understanding the behavior of functions helps us analyze their outputs and make predictions. One such function, f(x) = 2(3)^x, raises the question: What best describes its range? In this article, we will explore the range of the function f(x) = 2(3)^x, unveiling its behavior and identifying the set of possible output values. Join us as we dive into the world of mathematical functions and discover the range of this particular exponential function.

 

1. Defining the Function f(x) = 2(3)^x:

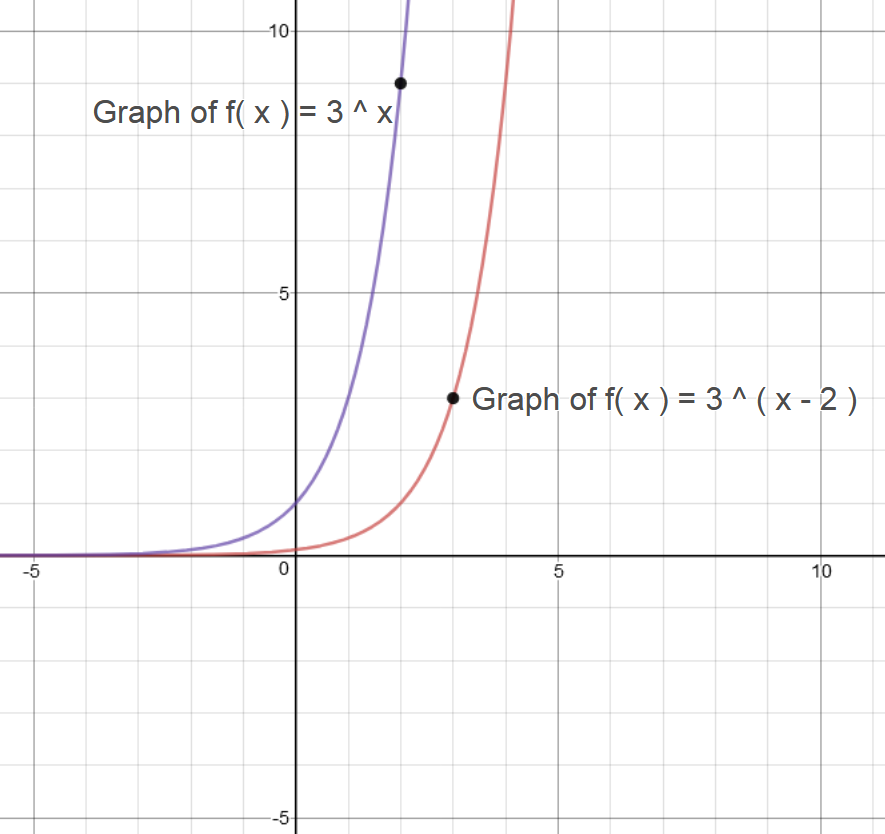
Function f(x)

 

The function f(x) = 2(3)^x is an exponential function.

 

It involves the variable x as an exponent on the base of 3, multiplied by the coefficient 2.

 

This function represents a mathematical relationship where the output value, f(x), depends on the input value, x.

 

2. Exponential Growth:

The function f(x) = 2(3)^x exhibits exponential growth. As the input value, x, increases, the output value, f(x), grows rapidly.

 

The exponential growth is determined by the base, which in this case is 3.

 

Each increment in the value of x results in a significant increase in the value of f(x).

 

3. Positive and Negative Values:

The function f(x) = 2(3)^x can produce both positive and negative values, depending on the input value, x.

 

When x is a positive integer, the output value, f(x), will also be positive.

 

However, when x is a negative integer, the output value will be a fraction or decimal, resulting in a negative f(x) value.

 

4. Increasing Function:

The function f(x) = 2(3)^x is an increasing function.

 

This means that as the input value, x, increases, the output value, f(x), also increases.

 

The rate of increase depends on the base, 3, which amplifies the exponential growth.

 

The function does not exhibit any intervals where the output values decrease.

 

5. Range of the Function:

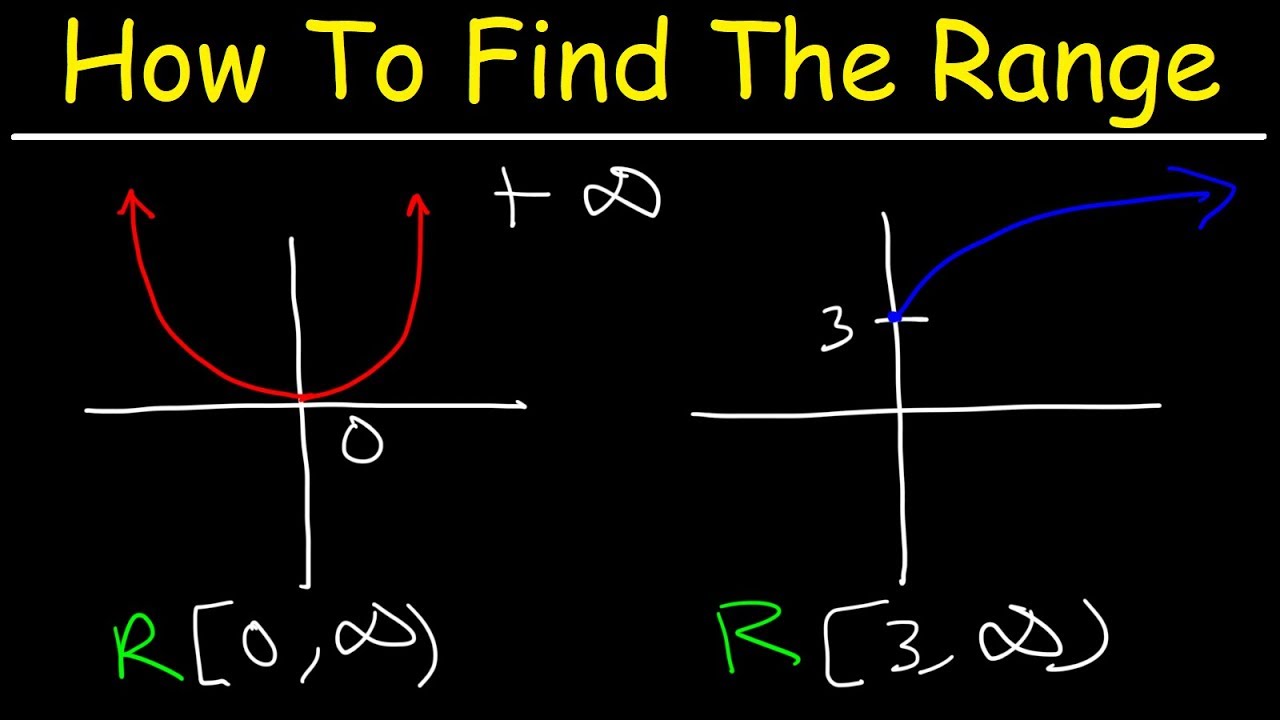
Range of the Function

 

The range of the function f(x) = 2(3)^x includes all positive real numbers and zero.

 

Since the base, 3, is positive, the function always produces positive output values.

 

However, the range does not include any negative numbers or fractions.

 

The function approaches zero as x approaches negative infinity but never reaches negative values or fractions.

 

6. Unbounded Growth:

The function f(x) = 2(3)^x exhibits unbounded growth. As x increases without bound, the output values of f(x) also increase without bound.

 

This means that there is no maximum value that f(x) can reach.

 

However, the function approaches zero as x approaches negative infinity, indicating that it does have a lower bound of zero.

 

7. Application Examples:

The function f(x) = 2(3)^x has various applications in real-world scenarios.

 

It can describe population growth, investment returns, or the decay of radioactive substances.

 

In each case, the function's exponential growth or decay behavior helps analyze and predict the changes in the system being modeled.

 

The function f(x) = 2(3)^x is an exponential function that exhibits rapid and unbounded growth. Its range includes all positive real numbers and zero. The function does not produce negative output values or fractions. Understanding the behavior and range of this function is crucial for analyzing and predicting its outputs in various mathematical and real-world applications. By unraveling the characteristics of the function f(x) = 2(3)^x, we gain insights into the fascinating world of exponential growth and the mathematical relationships that shape our understanding of the natural and physical phenomena around us.