Determining the Ordered Pair That Satisfies Two Inequalities: y > –3x + 3 and y > 2x – 2

In the realm of mathematics, solving inequalities plays a vital role in understanding and analyzing various mathematical expressions. This article aims to address a specific problem: finding the ordered pair that satisfies two given inequalities. The inequalities in question are y > –3x + 3 and y > 2x – 2. By applying fundamental principles and techniques, we will demonstrate how to determine the ordered pair that makes both inequalities true. By the end of this article, you will have a clear understanding of the steps involved in solving such problems.

I. Understanding Inequalities:

Before delving into the specifics of solving the given inequalities, it is crucial to establish a solid understanding of inequalities themselves. Inequalities represent relationships between two expressions that are not equal. The symbols used in inequalities are greater than (>), less than (<), greater than or equal to (≥), and less than or equal to (≤). In our case, we have two inequalities: y > –3x + 3 and y > 2x – 2.

Understanding Inequalities

II. Solving the First Inequality: y > –3x + 3:

To solve the first inequality, y > –3x + 3, we will follow a step-by-step approach. First, we will rewrite the inequality in slope-intercept form, y = mx + b, where m represents the slope and b represents the y-intercept. In this case, the equation becomes y = –3x + 3. By examining the slope, we determine that the line is downward sloping.

Next, we will graph the inequality on a coordinate plane. By plotting the y-intercept and using the slope to determine additional points, we can draw a line representing the inequality. To determine which side of the line satisfies the inequality, we will perform a test point calculation. By substituting the coordinates of a test point into the inequality, we can determine if it satisfies the given condition.

Finally, we shade the region above the line to represent the solutions to the inequality.

III. Solving the Second Inequality: y > 2x – 2:

Similarly, we will now focus on solving the second inequality, y > 2x – 2. Following the same steps as before, we rewrite the inequality in slope-intercept form: y = 2x – 2. The slope in this case is positive, indicating an upward sloping line.

We graph the inequality by plotting the y-intercept and using the slope to find additional points. The test point calculation helps us determine which side of the line satisfies the inequality. Once again, we shade the region above the line to represent the solutions to the inequality.

IV. Finding the Common Solutions:

Having graphed both inequalities, we now seek the ordered pair that satisfies both conditions simultaneously. This can be achieved by identifying the overlapping region on the graph.

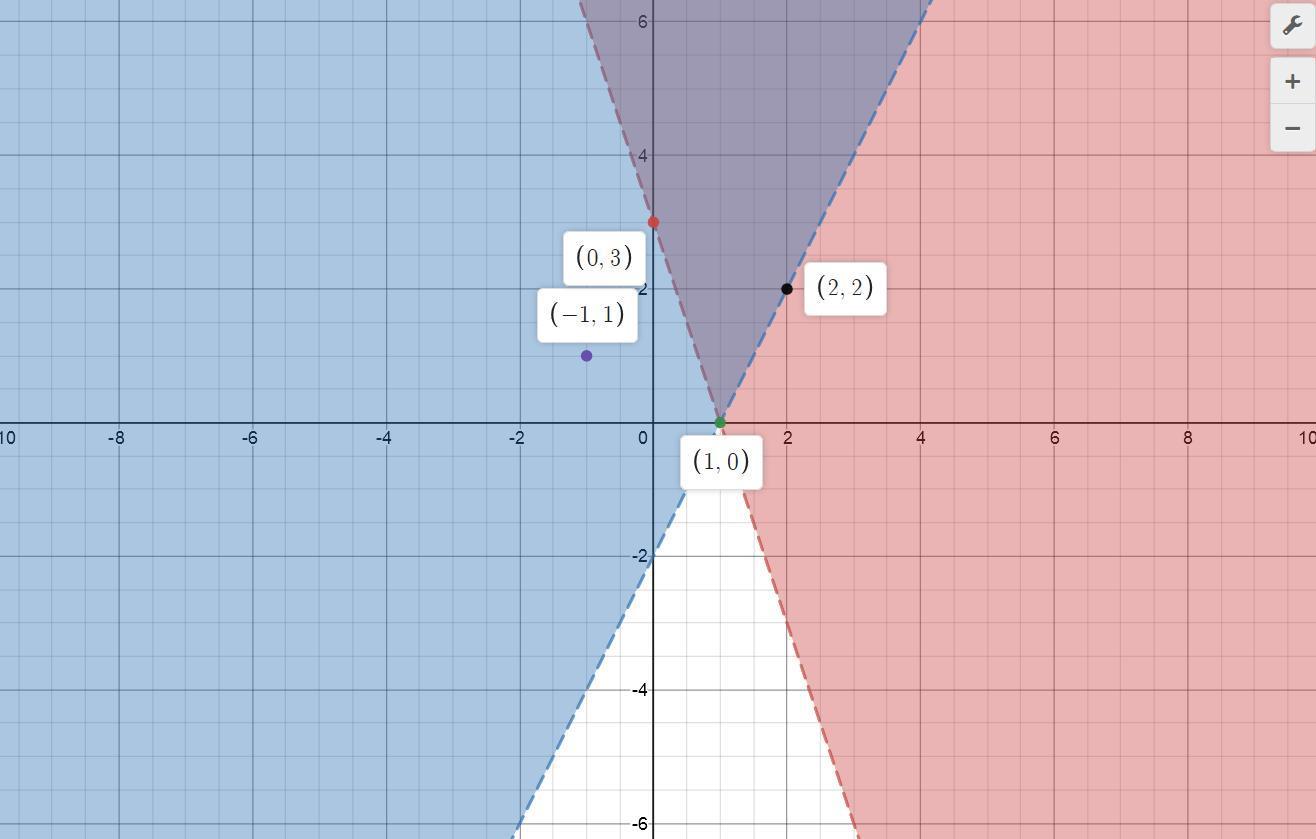
Graphed both inequalities

By considering the shaded areas from both inequalities, we can determine the common solution that makes both y > –3x + 3 and y > 2x – 2 true. The ordered pair within the overlapping region represents the solution to the problem at hand.

V. Conclusion:

In this article, we explored the process of determining the ordered pair that satisfies two given inequalities, y > –3x + 3 and y > 2x – 2. By understanding the fundamental principles of inequalities and employing a step-by-step approach, we successfully solved each inequality and graphed the corresponding lines on a coordinate plane.

Finally, by identifying the overlapping region, we found the common solution that makes both inequalities true. Solving inequalities is a crucial skill in mathematics, and by following the techniques outlined in this article, you can confidently approach similar problems in the future.