The Most Sided Shape: Exploring the World of Polygons
Shapes are fundamental elements in geometry, and polygons are a key category within this realm. While there are numerous polygons with different numbers of sides, one question that often arises is: "What is the most sided shape?" In this article, we will explore the concept of the most sided shape, discussing polygons with a high number of sides and their unique characteristics. By delving into the world of polygons, we aim to unveil the intriguing nature of these geometric wonders.
1. Understanding Polygons
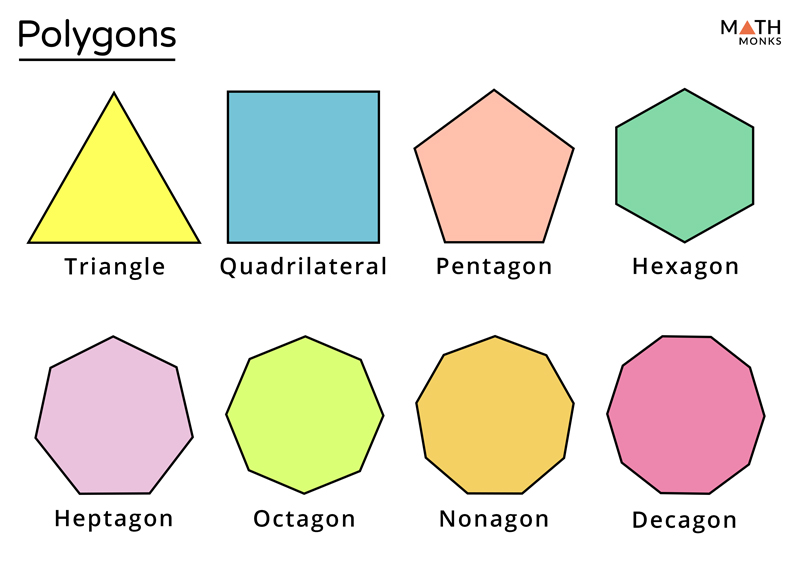
Polygons
Polygons are closed two-dimensional shapes composed of straight sides and angles. They are formed by connecting three or more line segments.
Polygons play a vital role in various mathematical and real-world applications, providing a foundation for concepts such as area, perimeter, and symmetry.
2. Common Polygons
Before exploring the concept of the most sided shape, let's review some common polygons that are widely recognized and studied.
These include the triangle (3 sides), quadrilateral (4 sides), pentagon (5 sides), hexagon (6 sides), and octagon (8 sides). Each of these polygons has its own distinct properties and characteristics.
3. High-Sided Polygons
As the number of sides increases, polygons become more complex and intricate.
Higher-sided polygons are less commonly encountered in everyday life, but they continue to captivate mathematicians and geometry enthusiasts.
Let's explore some examples of high-sided polygons and their unique features.
4. Heptagon (7-sided Polygon)
The heptagon, also known as the septagon, is a polygon with seven sides. It is an interesting shape due to its asymmetry and the variety of angles it contains.
While regular heptagons have equal side lengths and angles, irregular heptagons can exhibit different side lengths and angles.
5. Nonagon (9-sided Polygon)
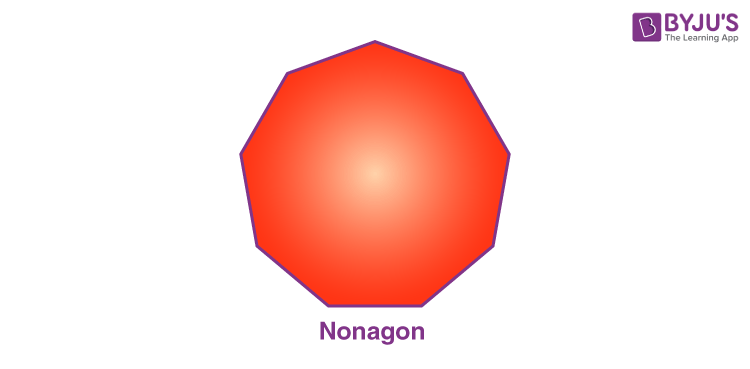
Nonagon (9-sided Polygon)
The nonagon, also referred to as the enneagon, is a polygon with nine sides. It is characterized by its nine angles and nine vertices. Like other polygons, nonagons can be regular or irregular, depending on the equality of their sides and angles.
6. Decagon (10-sided Polygon)
The decagon is a polygon with ten sides. It is a symmetrical shape with ten equal angles and ten vertices. The regular decagon has equal side lengths, while irregular decagons can have varying side lengths and angles.
7. Dodecagon (12-sided Polygon)
The dodecagon is a polygon with twelve sides. It is known for its twelve equal angles and twelve vertices. The regular dodecagon has twelve equal side lengths, while irregular dodecagons can exhibit different side lengths and angles.
8. N-gons: Polygons with Arbitrary Sides
The term "n-gon" is used to refer to a polygon with an arbitrary number of sides. It allows for a generalization of polygons beyond specific numbers of sides.
For example, a 15-sided polygon would be referred to as a 15-gon. The properties and characteristics of n-gons can vary widely based on the number of sides.
9. Circle: An Infinite-Sided Polygon
While polygons typically have a finite number of sides, it is worth mentioning that a circle can be considered a polygon with an infinite number of sides.
Although circles are distinct from polygons in many aspects, they share some fundamental geometric properties.
In the world of polygons, the concept of the most sided shape leads us to explore polygons with a high number of sides. While polygons with three, four, five, and even eight sides are commonly encountered, higher-sided polygons become more intricate and less frequently encountered. Shapes like the heptagon, nonagon, decagon, and dodecagon offerintriguing examples of polygons with unique properties. Additionally, the concept of n-gons allows for a generalization of polygons beyond specific numbers of sides. Finally, while not traditionally considered a polygon, the circle can be seen as a polygon with an infinite number of sides.
Understanding the characteristics and properties of polygons with a high number of sides enriches our knowledge of geometry and mathematics. It showcases the diversity and complexity that can arise from the simple concept of connecting line segments. The exploration of polygons and their various properties fosters curiosity and appreciation for the elegance of mathematical concepts.