Finding the Radius of a Circle with the Equation x^2 + y^2 = z

The equation x^2 + y^2 = z represents a circle in the Cartesian coordinate system. Understanding how to find the radius of a circle given this equation is crucial in geometry and mathematical applications. In this article, we will explore the process and concepts behind finding the radius when the equation of a circle is in the form x^2 + y^2 = z. Join us as we dive into the world of circles and uncover the steps to determine their radii.

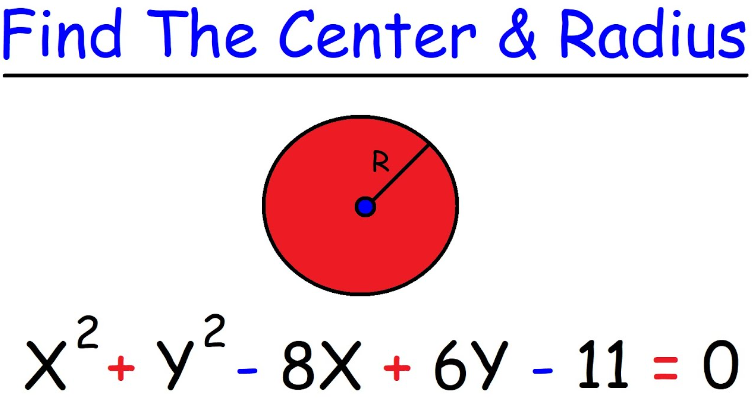
Example find the center and radius

1. Understanding the Equation x^2 + y^2 = z:

The equation x^2 + y^2 = z represents a circle in the Cartesian coordinate plane, where (x, y) are the coordinates of a point on the circle and z represents a constant value.

This equation is derived from the Pythagorean theorem, where the sum of the squares of the distances from any point (x, y) on the circle to the origin (0, 0) is equal to z.

2. The Relationship between the Equation and the Circle's Radius:

To find the radius of a circle when the equation is in the form x^2 + y^2 = z, we can observe that the radius is the square root of z.

This is because the equation represents all the points (x, y) that are equidistant from the origin (0, 0) with a distance equal to the square root of z.

Hence, the square root of z gives us the radius of the circle.

3. Steps to Find the Radius:

To determine the radius of a circle given the equation x^2 + y^2 = z, follow these steps:

a. Identify the value of z in the equation.

b. Take the square root of z to obtain the radius.

4. Example: Let's consider an example to illustrate the process.

Suppose we have the equation x^2 + y^2 = 25. To find the radius of this circle, we follow these steps:

a. Identify the value of z: In this case, z = 25.

b. Take the square root of 25: √25 = 5.

Therefore, the radius of the circle is 5 units.

5. Additional Considerations:

It's important to note that the equation x^2 + y^2 = z represents circles centered at the origin (0, 0). If the equation is in the form (x - h)^2 + (y - k)^2 = r^2, where (h, k) represents the center of the circle and r is the radius, the process to find the radius is different. In such cases, the radius is simply equal to r.

Student solving math

When the equation of a circle is given in the form x^2 + y^2 = z, the radius of the circle can be determined by taking the square root of z. This equation represents all the points equidistant from the origin with a distance equal to the square root of z. By following the steps outlined in this article, you can easily find the radius of a circle when its equation is in this form. Understanding this concept is fundamental in geometry and various mathematical applications.