Which Shows the Following Expression After the Negative Exponents Have Been Eliminated? Demystifying Exponential Operations

Exponents play a crucial role in mathematics, allowing us to express repeated multiplication and simplify complex equations. However, when negative exponents come into play, the expression can become confusing. In this article, we will unravel the mystery of negative exponents and explore the process of eliminating them to simplify expressions. Join us as we demystify exponential operations and reveal the expression that emerges after the negative exponents have been eliminated.

Solve fractions problem

I. Understanding Exponents and Negative Exponents:

a. Exponents Basics: Exponents represent the number of times a base number is multiplied by itself. For example, in the expression 2^3, the base number 2 is multiplied by itself three times, resulting in 2 * 2 * 2 = 8.

b. Negative Exponents: Negative exponents arise when we have a reciprocal of a number raised to a positive exponent. For instance, 2^-3 is equivalent to 1/(2^3), which is 1/8.

II. Eliminating Negative Exponents:

a. Applying the Rule: To eliminate negative exponents, we can apply the rule that states a negative exponent is equivalent to the reciprocal of the base raised to the positive exponent. In other words, x^-n is equal to 1/(x^n).

b. Reciprocal Conversion: By converting negative exponents into their reciprocal form, we can transform the expression into a positive exponent.

III. Simplifying Expressions with Negative Exponents:

a. Example 1:

Let's consider the expression (3^2) / (2^-4). To eliminate the negative exponent, we convert 2^-4 into its reciprocal form, which is 1/(2^4). The expression then becomes (3^2) / (1/(2^4)). Simplifying further, we can rewrite it as (3^2) * (2^4). Evaluating the exponents, we have 9 * 16 = 144.

b. Example 2:

Another example is the expression (5^3) * (4^-2) / (2^-1). We convert 4^-2 and 2^-1 into their reciprocal forms, which are 1/(4^2) and 1/(2^1), respectively. The expression becomes (5^3) * (1/(4^2)) / (1/(2^1)). Simplifying, we have (5^3) * (1/16) / (1/2). Simplifying further, we obtain (5^3) * (2/16), which is equivalent to (5^3) * (1/8).

IV. The Expression After Eliminating Negative Exponents:

After eliminating negative exponents from an expression, we obtain a simplified form that consists of positive exponents and their corresponding operations. The specific expression will depend on the original equation and the exponents involved.

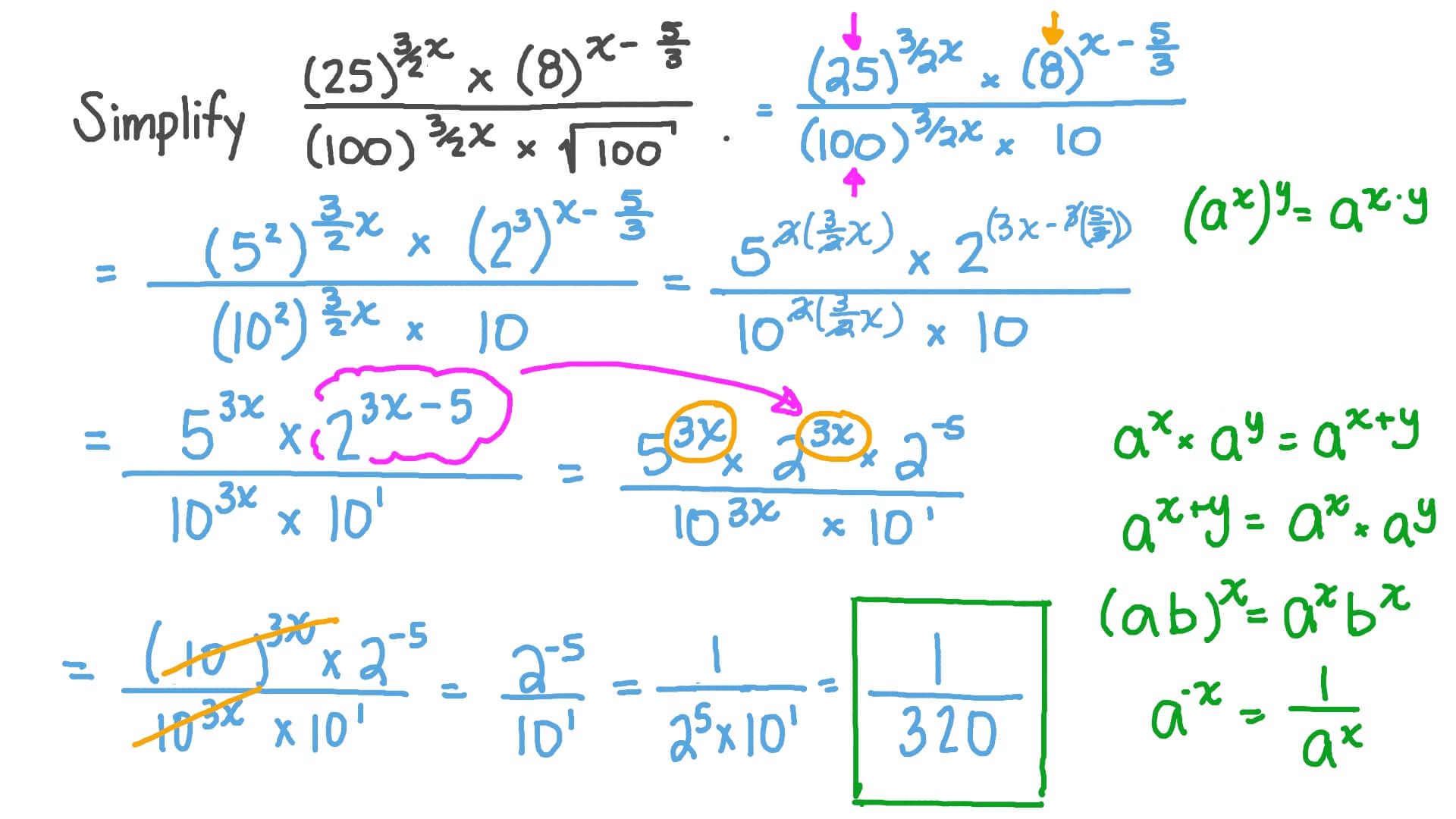
Do the maths Simplify

Negative exponents can initially appear daunting, but by applying the rule of converting them into their reciprocal form, we can simplify expressions and eliminate the confusion. Understanding the process of eliminating negative exponents allows us to transform complex equations into more manageable forms. By demystifying exponential operations and effectively handling negative exponents, we can confidently navigate mathematical expressions and arrive at the desired results.